Matched Filtering
The GW fluctuations are very tiny. For a 4km interferometer the strongest fluctuations are 1000 times smaller than the diameter of a proton. At these length scales it is hard to get rid of all the noise and random fluctuations. Pressure from photons becomes relevant.The GW signals even if they are recorded will be buried in the noise generated by the detector components and surrounding environment.
A matched filtering technique was suggested by Sanjeev Dhurandhar and B S Satyaprakash. The idea is to calculate templates for the wave and cross-correlate them with the data from the detector. If a signal similar to the template is present in the data the cross-correlation result will be able to identify it.
Templates of GW
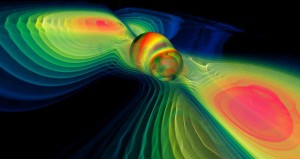
Numerical simulation of two merging black holes (Credit: Werner Benger)
A template is a description of the wave. It shows the amplitude and frequency of the wave. The matched filtering works only if we know the exact template of GW signals. A major part of GW physics is to correctly model astrophysical sources and calculate what the waves will look like.
Einstein’s field equation is numerically solved to obtain the geometry around merging blackholes or neutron stars. If the geometry is known then it is possible to predict how they will move and what will happen consequently.
Exact wave-forms of GW can then be generated.
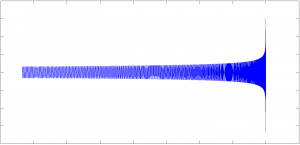
GW signal from compact binary coalescence using SEOBNRv2 (Credit: Bhooshan Gadre)
GW Radiometry
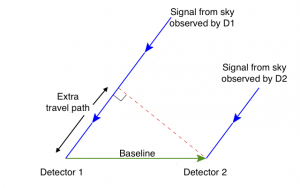
Basic principle of GW radiometry (Credit: Anirban Ain)
GW Radiometry is similar to Radio Interferometry which is extensively used in radio astronomy. The basic idea is that signals from different directions of the sky reaches different detectors at different times. If we correctly know the relative locations of the detecters we can use that information to identify the direction of the source.
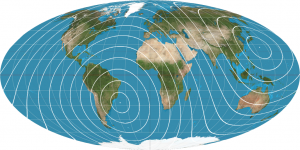
Projected contours of equal time delay (Credit: Anirban Ain, Background image: Daniel R. Strebe)
Only this information is incomplete because for one baseline signal from multiple directions can have same time delay. This ambiguity is settled by using the rotation of the earth. As the earth rotates the base line and thus the contours of equal time delay changes and a full day worth of data becomes enough to map the entire sky.
Detector Characterisation
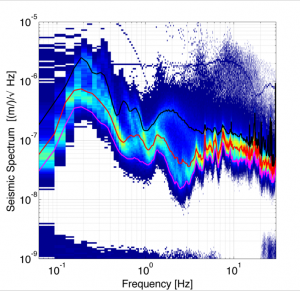
Histogram of seismic noise from LIGO Livingston (Credit: N. Mukund, M. Coughlin, J. Harms et al)
Detector characterization is crucial both for operating the instrument at its desired sensitivity and for estimating the significance of GW events at the time of detection. Advanced LIGO has an extensive physical environment monitoring system comprising of seismometers, microphones, magnetometers, voltage monitors, temperature sensors etc that look for possible non-astrophysical contamination of the strain data.
Electro Magnetic Follow-up
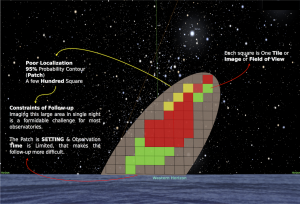
Scanning strategies for EM Followup(Credit: Javed Rana, Background:Stellarium)
The detection of electromagnetic (EM) counterparts of GW will help immensely in characterizing its source, probing the nature of counterparts associated with compact binary coalescence, and enriching our understanding of their environments. The localized error regions (or patches) in the sky obtained from observations by GW detectors will be a few tens to a few hundreds of square-degrees wide, and may not be observable in a single night using a ground-based optical telescope. It is important to developed an algorithm to tile the patch, optimize the observing sequence, and maximize the probability of finding the EM counterpart.
A poster on the research in IUCAA can be found here.
